Backtracking — 回溯法

發表於 更新於 分類於
回溯法是暴力破解法的一種，在列出各種可能的組合時，如果遇到不符合條件的就不再繼續向下查找，而是回到上層繼續尋找其他可能，聽起來有點抽象，可以想像有很多條岔路可以做選擇，不過已經知道有些岔路不會得到我們需要的結果，就沒有必要繼續往下找，而是折返到上個路口，繼續探索其他還沒訪問過的岔…

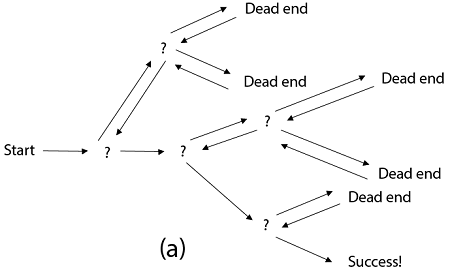
回溯法是暴力破解法的一種，在列出各種可能的組合時，如果遇到不符合條件的就不再繼續向下查找，而是回到上層繼續尋找其他可能，聽起來有點抽象，可以想像有很多條岔路可以做選擇，不過已經知道有些岔路不會得到我們需要的結果，就沒有必要繼續往下找，而是折返到上個路口，繼續探索其他還沒訪問過的岔路，如同下圖所示

在理解回溯法之前需要先認識 permutation 排列法

甚麼是 permutation 排列法?

是將相異物件或符號根據確定的順序重排。每個順序都稱作一個置換或排列。例如，從一到六的數字有 720 種排列，對應於由這些數字組成的所有不重複亦不闕漏的序列，例如4, 5, 6, 1, 2, 3 與1, 3, 5, 2, 4, 6。(引用自 wikipedia)

假設現在有個字串 ABC，試問會有幾種排列組合? 所有可能的排列組合如下圖，可以推論出公式 = 階乘

Ex.字串長度為 3 的話，就會有 3*2*1=6 種可能

用 js 實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const arr = ["A", "B", "C"];

const permutation = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      for (let k = 0; k < arr.length; k++) {
        if (i === j || j === k || k === i) {
          continue;
        }
        console.log(arr[i], arr[j], arr[k]);
      }
    }
  }
};

permutation(arr);
//A B C
//A C B
//B A C
//B C A
//C A B
//C B A

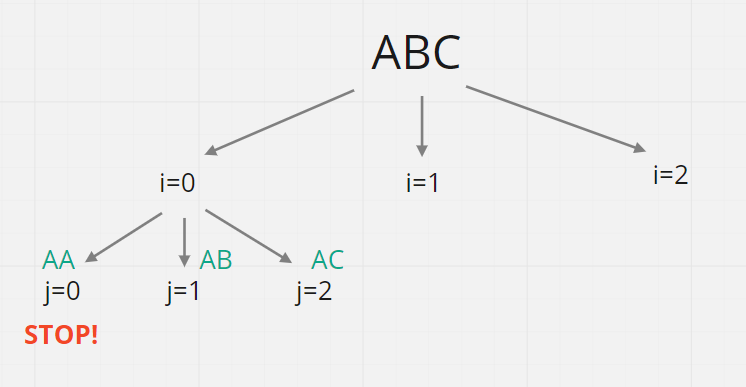
利用三個迴圈列出所有排列組合，假設字串當中任意兩個單字相同，就排除掉該組合，將程式流程畫成圖的話，會發現紫色三角形的範圍其實全部都不符合條件(非 ABC 的排列組合)

因此在 i = 0, j = 0 的時候就要喊停了，回溯到 i = 0 這一個步驟，這個中斷向下查找往回走的動作就是 Backtracking

提早設定中止條件，向上回溯的程式碼如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const arr = ["A", "B", "C"];
const permutation = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      if (i === j) {
        continue;
      }
      for (let k = 0; k < arr.length; k++) {
        if (j === k || k === i) {
          continue;
        }
        console.log(arr[i], arr[j], arr[k]);
      }
    }
  }
};

permutation(arr);

嘗試用雙指針的概念來解這題，利用 start 與 i 兩個指針互換位置來取得不同的排列組合，執行的步驟如下

  1. start 跟 i 都從 0 開始
  • start = 0，i = 0，獲得以 A 為開頭的組合，ex. ABC
  1. i 前進一格之後與 start 交換位置
  • start = 0，i = 1，獲得以 B 為開頭的組合，ex. BAC
  1. i 前進一格之後與 start 交換位置
  • start = 0，i = 2，獲得以 C 為開頭的組合，ex. CBA

當 i = 2 的時候意謂著 i 指針已經走到最後一步，這時 start 指針必須前進一步，i 指針則退回與 start 指針相同的位置，依循先前的規則，start 和 i 兩個指針所指向的字母作交換，交換完畢後 i + 1

字串 ABC

  • start = 1，i = 1，兩個指針指向同個字母，交換後維持不變，依然是 ABC
  • start = 1，i = 2，兩個指針互換後，獲得 ACB

字串 BAC

  • start = 1，i = 1，兩個指針指向同個字母，交換後維持不變，依然是 BAC
  • start = 1，i = 2，兩個指針互換後，獲得 BCA

字串 CBA

  • start = 1，i = 1，兩個指針指向同個字母，交換後維持不變，依然是 CBA
  • start = 1，i = 2，兩個指針互換後，獲得 CAB

用 js 實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
let result = [];
const permutation = (arr, start) => {
  if (start >= arr.length) {
    //因為arr最後會被換回原本的字串ABC 需要用淺拷貝的方式複製當下已經交換過的陣列
    result.push([...arr]);
  } else {
    for (let i = start; i < arr.length; i++) {
      //將start與i作交換
      swap(arr, start, i);

      permutation(arr, start + 1);

      //交換完之後要再換回來才會是原本的字串ABC
      swap(arr, start, i);
    }
  }
};

const swap = (arr, n1, n2) => {
  [arr[n1], arr[n2]] = [arr[n2], arr[n1]];
};

permutation(["A", "B", "C"], 0);
console.log("result", result);

執行結果如下